Continuous Strictly Concave Utility Function Unique Solution

Negative of a convex function

In mathematics, a concave function is the negative of a convex function. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap, or upper convex.

Definition [edit]

A real-valued function ${\displaystyle f}$ on an interval (or, more generally, a convex set in vector space) is said to be concave if, for any ${\displaystyle x}$ and ${\displaystyle y}$ in the interval and for any ${\displaystyle \alpha \in [0,1]}$ ,^[1]

${\displaystyle f((1-\alpha )x+\alpha y)\geq (1-\alpha )f(x)+\alpha f(y)}$

A function is called strictly concave if

${\displaystyle f((1-\alpha )x+\alpha y)>(1-\alpha )f(x)+\alpha f(y)\,}$

for any ${\displaystyle \alpha \in (0,1)}$ and ${\displaystyle x\neq y}$ .

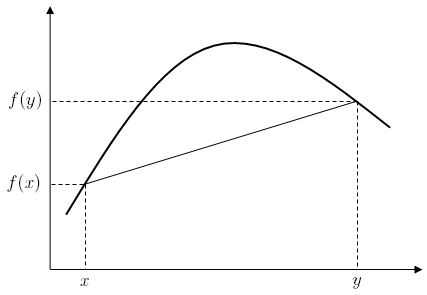
For a function ${\displaystyle f:\mathbb {R} \to \mathbb {R} }$ , this second definition merely states that for every ${\displaystyle z}$ strictly between ${\displaystyle x}$ and ${\displaystyle y}$ , the point ${\displaystyle (z,f(z))}$ on the graph of ${\displaystyle f}$ is above the straight line joining the points ${\displaystyle (x,f(x))}$ and ${\displaystyle (y,f(y))}$ .

A function ${\displaystyle f}$ is quasiconcave if the upper contour sets of the function ${\displaystyle S(a)=\{x:f(x)\geq a\}}$ are convex sets.^[2]

Properties [edit]

Functions of a single variable [edit]

1. A differentiable function f is (strictly) concave on an interval if and only if its derivative function f ′ is (strictly) monotonically decreasing on that interval, that is, a concave function has a non-increasing (decreasing) slope.^{[3] [4]}
2. Points where concavity changes (between concave and convex) are inflection points.^[5]
3. If f is twice-differentiable, then f is concave if and only if f ′′ is non-positive (or, informally, if the "acceleration" is non-positive). If its second derivative is negative then it is strictly concave, but the converse is not true, as shown by f(x) = −x ⁴ .
4. If f is concave and differentiable, then it is bounded above by its first-order Taylor approximation:^[2]

   $${\displaystyle f(y)\leq f(x)+f'(x)[y-x]}$$

   

5. A Lebesgue measurable function on an interval C is concave if and only if it is midpoint concave, that is, for any x and y in C

   $${\displaystyle f\left({\frac {x+y}{2}}\right)\geq {\frac {f(x)+f(y)}{2}}}$$

   

6. If a function f is concave, and f(0) ≥ 0, then f is subadditive on ${\displaystyle [0,\infty )}$ . Proof:
   • Since f is concave and 1 ≥ t ≥ 0, letting y = 0 we have

     $${\displaystyle f(tx)=f(tx+(1-t)\cdot 0)\geq tf(x)+(1-t)f(0)\geq tf(x).}$$

     

   • For ${\displaystyle a,b\in [0,\infty )}$ :

     $${\displaystyle f(a)+f(b)=f\left((a+b){\frac {a}{a+b}}\right)+f\left((a+b){\frac {b}{a+b}}\right)\geq {\frac {a}{a+b}}f(a+b)+{\frac {b}{a+b}}f(a+b)=f(a+b)}$$

     

Functions of n variables [edit]

1. A function f is concave over a convex set if and only if the function −f is a convex function over the set.
2. The sum of two concave functions is itself concave and so is the pointwise minimum of two concave functions, i.e. the set of concave functions on a given domain form a semifield.
3. Near a local maximum in the interior of the domain of a function, the function must be concave; as a partial converse, if the derivative of a strictly concave function is zero at some point, then that point is a local maximum.
4. Any local maximum of a concave function is also a global maximum. A strictly concave function will have at most one global maximum.

Examples [edit]

Applications [edit]

• Rays bending in the computation of radiowave attenuation in the atmosphere involve concave functions.
• In expected utility theory for choice under uncertainty, cardinal utility functions of risk averse decision makers are concave.
• In microeconomic theory, production functions are usually assumed to be concave over some or all of their domains, resulting in diminishing returns to input factors.^[7]

See also [edit]

• Concave polygon
• Jensen's inequality
• Logarithmically concave function
• Quasiconcave function
• Concavification

References [edit]

1. ^ Lenhart, S.; Workman, J. T. (2007). Optimal Control Applied to Biological Models. Mathematical and Computational Biology Series. Chapman & Hall/ CRC. ISBN978-1-58488-640-2.
2. ^ ^{a b} Varian, Hal R. (1992). Microeconomic analysis (3rd ed.). New York: Norton. p. 489. ISBN0-393-95735-7. OCLC 24847759.
3. ^ Rudin, Walter (1976). Analysis. p. 101.
4. ^ Gradshteyn, I. S.; Ryzhik, I. M.; Hays, D. F. (1976-07-01). "Table of Integrals, Series, and Products". Journal of Lubrication Technology. 98 (3): 479. doi:10.1115/1.3452897. ISSN 0022-2305.
5. ^ Hass, Joel (13 March 2017). Thomas' calculus. Heil, Christopher, 1960-, Weir, Maurice D.,, Thomas, George B., Jr. (George Brinton), 1914-2006. (Fourteenth ed.). [United States]. p. 203. ISBN978-0-13-443898-6. OCLC 965446428.
6. ^ Cover, Thomas M.; Thomas, J. A. (1988). "Determinant inequalities via information theory". SIAM Journal on Matrix Analysis and Applications. 9 (3): 384–392. doi:10.1137/0609033. S2CID 5491763.
7. ^ Pemberton, Malcolm; Rau, Nicholas (2015). Mathematics for Economists: An Introductory Textbook. Oxford University Press. pp. 363–364. ISBN978-1-78499-148-7.

Further References [edit]

• Crouzeix, J.-P. (2008). "Quasi-concavity". In Durlauf, Steven N.; Blume, Lawrence E (eds.). The New Palgrave Dictionary of Economics (Second ed.). Palgrave Macmillan. pp. 815–816. doi:10.1057/9780230226203.1375. ISBN978-0-333-78676-5.
• Rao, Singiresu S. (2009). Engineering Optimization: Theory and Practice. John Wiley and Sons. p. 779. ISBN978-0-470-18352-6.

condetrushe.blogspot.com

Source: https://en.wikipedia.org/wiki/Concave_function

Share this post